学習指導の効果測定には、模試や外部検定のデータを用いて分布の変化を捉える必要があるのは昨日の記事で申し上げた通りです。
一般的に利用されている平均点の推移で捉える方法では、層別の動きが捉えられませんし、上下への動きが相殺して平均値の変動は小さなものに集約されてしまうこともあります。
追記:Excel 2016から箱ひげ図の作成機能が実装されています。使い方は「箱ひげ図を作成する」(Officeのサポート)をご参照ください。
❏ 箱ひげ図で、分布の変化とクラス間での相違を捉える
層別の分布を知る必要に加えて、クラスごと、担当教員ごとに指導の成果は異なりますので、差分を捉えるため、クラスを並べて比較する必要もあります。
そのために便利なのが、昨日の記事に掲載した箱ひげ図です。
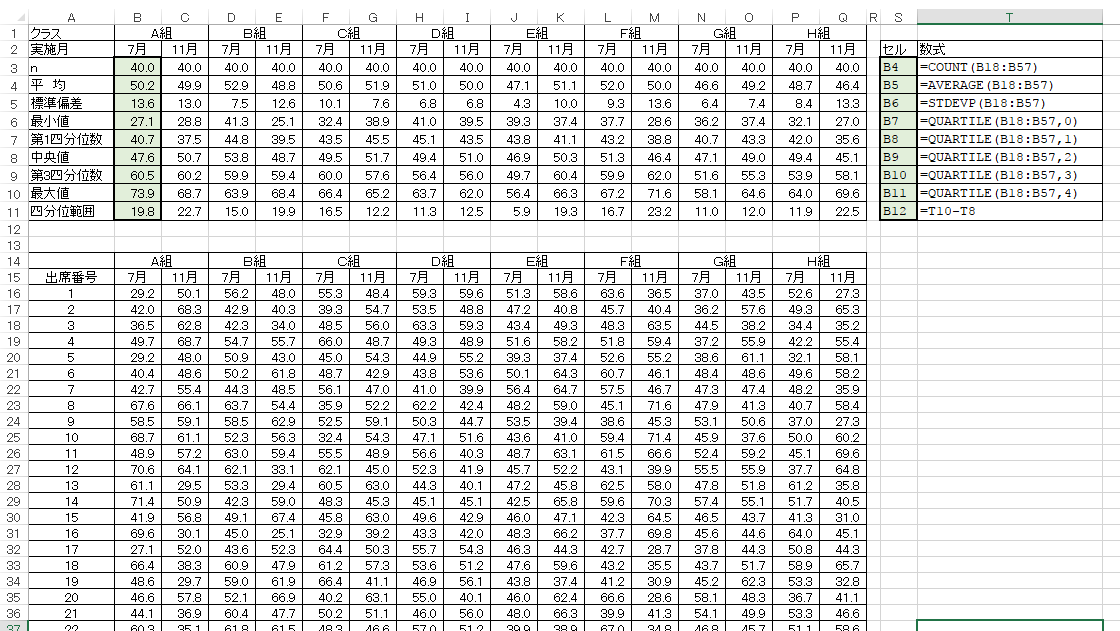
箱ひげ図では、得点をトップから最下位までずらりと並べて順位で4分割し、それぞれを以下のように表示するものです。
| 最大値(トップ) | 上方に伸びる「ひげ」の先端 |
| 上位25%(第3四分位数) | 箱の上端 |
| 中央値 | 箱内のグレーの濃淡の境界 |
| 下位25%(第1四分位数) | 箱の下端 |
| 最小値(ボトム) | 下方に伸びる「ひげ」の先端 |
なお、ひげの長さは、箱の高さ(=四分位範囲、IQR)の1.5倍までとするなど様々なルールがありますが、どの方法でもひげの範囲を超えたものは「外れ値」として扱います。
❏ 箱ひげ図から読み取れること
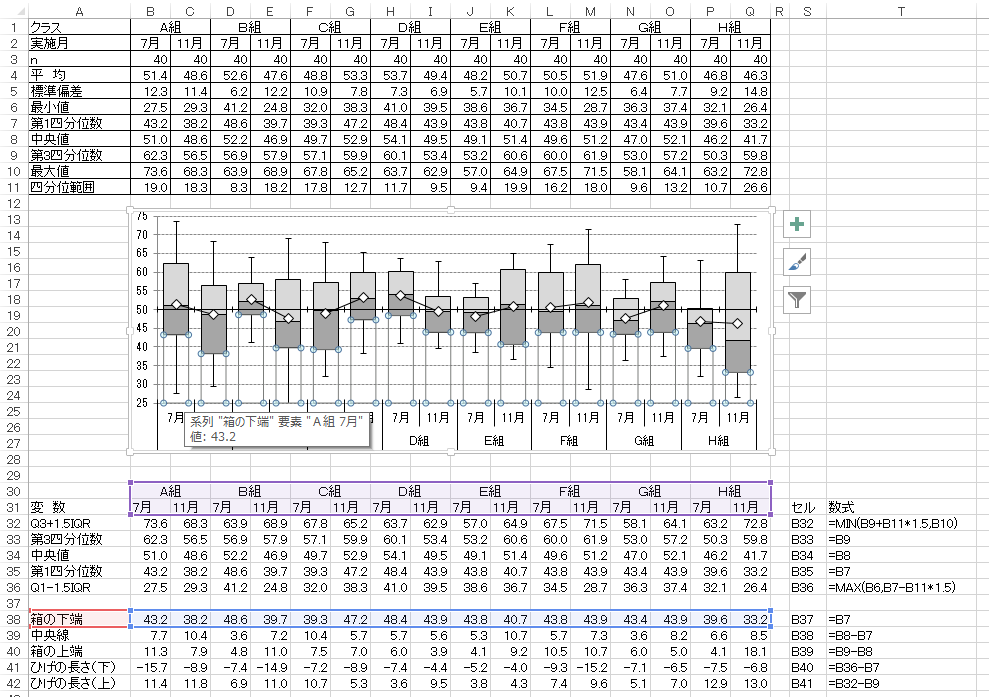
B組は、箱の上端の位置は7月と11月であまり変わりませんが、上方のひげは伸びており、最上位層の成績に伸長があったようです。しかしながら、中央値や箱の下端、下方のひげの先端は下がっており、最上位以外の生徒の成績は下降したことがわかります。
C組は、B組と反対に、中央値以下の四分位数に上昇があり、中位層、下位層の底上げはできた一方で、上位層に停滞や後退があったということになります。
クラス間での比較を箱ひげ図を用いて行うことで、そこで行われてきた指導が、どの層に対して効果的であったか探ることができます。
C組の実践から下位を支えるために有効な指導法を抽出できる可能性がありますし、B組で上位層に効果を上げた方法は、上位生向けの特別講習に転用したり、そこで与えた課題は任意の挑戦課題として用いていくという方法もありそうです。
❏ エクセルを使って箱ひげ図を作ってみる
箱ひげ図は、エクセルのグラフウイザードには含まれていないので、いざ作ろうとするとちょっとした工夫が必要です。
色々な方法がありますが、上のグラフは、積み上げ縦棒グラフ(箱の部分)と、誤差範囲のオプションを使っています。また、平均値はマーカー付き折れ線グラフで追加しました。
以下はデータシートです。四分位数の算出にはエクセルに実装されているQUARTILE関数を用います。その他の記述統計量も関数を設定しておけばデータを入れ替えるだけで自動で算出されます。
ちょっと工夫が必要なのは、上下のひげを誤差範囲のオプションを使う部分でしょうか。
詳しくは、上記サンプルのエクセルファイルがこちらからダウンロードできますので、ご参考になさってください。
教科固有の知識や技能については、如上の方法で倣うべき優良実践の所在を特定できますが、生徒に訊いてみないとわからない学習者としての自己認識や、学びの場での振る舞い方や学習方策の獲得についても「成果を定量化する必要」があります。
生徒にYESと答えてもらいたい質問に続く。
シリーズのインデックスへ
教育実践研究オフィスF 代表 鍋島史一