2018年11月に実施された大学入学共通テストの試行テストの検証結果が大学入試センターのホームページで公開されています。既にご覧になられたと思いますが、本日のブログでは、結果分析で用いられていた出題評価の様々な方法を取り上げてみます。
校内で導入し、日常的に活用するには少々ハードルが高いものも含まれていますが、考査問題の妥当性を評価し、最適化を図るための手法として、その概要は知っておきたいところです。
2019/04/10 公開の記事を再アップデートしました。
❏ 平均得点率(平均正答率)と標準偏差
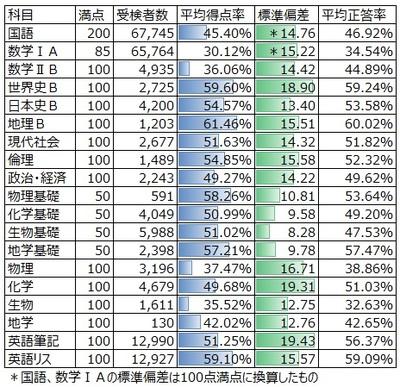
これらについては今さら説明は不要と思いますが、報告書の冒頭近くで登場するのは、全科目の平均得点一覧(報告書p.6-7)と科目ごとの得点分布のヒストグラム(同p.8-10)です。
報告書の中では、前者を指標に、こんな言い方をしています。
マーク式問題については、5割程度の平均得点率(平均正答率)を念頭に実施した。結果として平均得点率が5割程度以上となったのは、全19科目のうち7割を超える14科目であった。
平均点で出題の質や難度の適性にあたりをつけるのは、昔から採られている方法ですが、これらの数字だけで確かめることができるのは出題の質のごく一部であるのは言うまでもありません。
ちなみに、センター試験やその先祖である共通一次は目標平均点が60点でした。これからの生徒はより高いハードルに挑むことになります。定期考査問題もちょっと「スパイス」を加える必要がありそうです。
❏ ヒストグラムで点検する「有効得点レンジ」
平均点が最も高い地理Bと最も低い生物のヒストグラムを比較してみると、前者では20点未満のエリアが、後者では80点以上のエリアの分布は極めて少なく「ほぼ空白」であることが分かります。
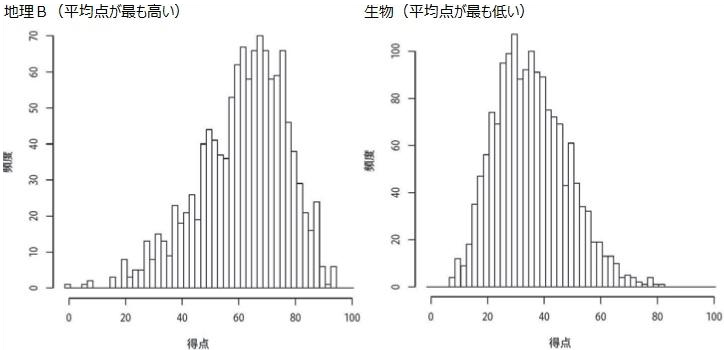
名目上100点満点のテストですが、いずれも実質的には80点分か、それ未満の短い得点スケールしか使えておらず、学力差が得点差に表れにくくなっています。
定期考査の場合は、不用意に赤点を出さないためにも、上位生の慢心を防ぐためにも、得点の上下をカットしたいという事情もあろうかと思いますが、選抜試験としては「識別力」(学力を点数に換算する性能)を優先すべきであり、得点スケールが目一杯使える問題が望まれます。
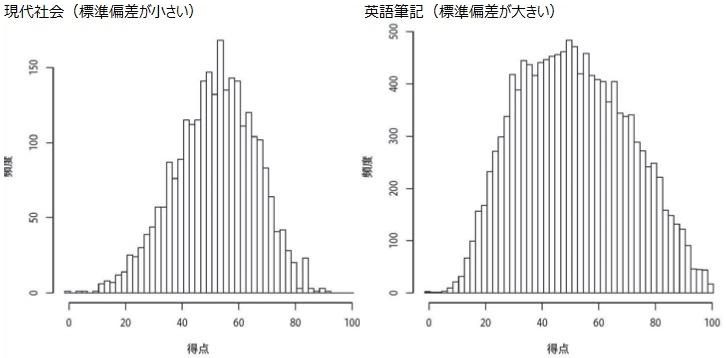
一方、下に並べた現代社会と英語筆記は、平均点はともに51点台、最頻値も似たような位置にありますが、標準偏差は、前者が13.40、後者は19.43とだいぶ違ったものになっています。
如上の識別力だけで言えば、より広いレンジを尺度として使える英語筆記の方が選抜試験の出題としては好ましいということになります。
❏ 設問正答率幹葉図で、硬軟のバランスを確かめる
なぜ、このような違いが出るかを知るには、報告書の中、p11以降に登場する「設問正答率幹葉図」をご覧いただくのが良いと思います。
設問正答率幹葉図とは、
平均正答率を5ポイント刻みで区切った区間を「幹」として縦に並べ、その右側に、各区間に含まれる設問の番号を、あたかも幹から伸びた「枝葉」のように列記して起こす図
を指します。下図は今回の日本史Bのものですが、正答率が9割を超えた設問から、10%に届かないものまで含まれていることが分かります。
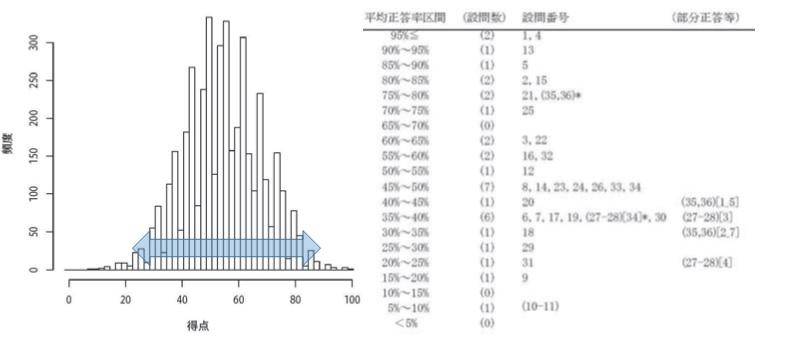
正答率が高い設問が多ければ、それらの問題で大部分の生徒が点数を拾ってしまうため、低得点域の分布がなくなります。上の例では20点以下の受験生はほとんどいません。
他方、低正答率の設問が一定程度以上含まれていると、高得点域の分布はつぶれてしまいます。ヒストグラムでも90点オーバーは僅少です。
昔からよく使われるワーディングに「硬軟取り混ぜて」というのがありますが、それも度を過ぎてしまうと、得点スケールを無駄に縮めてしまうリスクを招くということです。
同報告書の後半(p.57~)に掲載されている9段階のスタナインによる検証結果を見ても、日本史Bは最上位と最下位をのぞく7つの段階が、32点から78点の狭い範囲に「圧縮」されてしまっています。
赤点の生徒を出さないようにするのは、問題の細工ではなく、普段の授業への取り組ませ方ではないでしょうか。しっかりとした問題を作り、それを解けるように生徒を導いていくことが筋だと思います。
ここで紹介した手法以外にも、本報告書では以下のような方法で出題の評価を行っています。考査問題の妥当性検証を行うときにも、必要に応じて試してみては如何でしょうか。デジタル採点を導入している学校も増えつつあり、解析のためのデータも取得が容易になってきました。
誤肢選択率と正答選択率の比較(p.14など)
誤答を選択した者が、正答を選択したものを上回る設問も、何らかの問題を抱えていると考えられます。
五分位図のLo群とHi群の正答率の差(p.16など)
五分位図とは、当該科目の得点により、受検者を五群に等分割し、得点の低い順にLo群、LM群、M群、HM群、Hi群と名付け、各郡ごとの平均得点率を示したものを言います。ある設問において、Lo群とHi群の正答率の差が20%以下である場合、その設問は識別力がない(=好ましくない問題)とされます。
ピアソン相関を用いた検証(p.26)
科目の得点から当該設問を除いたものと当該設問との得点の相関を差します。今回の試行テストでは、ピアソン相関が0.1を下回り、他の設問との相関が低い問題が、国語や数学ⅡB、政経生物、地学で10%以上を占めていました。この手の問題は、本番では除外・改善されるはずです。
このシリーズのインデックスに戻る。
教育実践研究オフィスF 代表 鍋島史一
