前稿(その2)の終わりに、「改善に向けた新たな知見を得るのに最も効率的で確実な方法は、既に校内で高い評価を得ている先生の実践に倣うことであり、高評価を得た先生からの積極的な発信が期待される」と申し上げましたが、教科内/校内に向けて発信すべき実践の所在を知るには、個人票裏面の「クラス別集計」をご覧いただくのが好適です。
❏ 相対的な位置と、クラスごとの違いを確認
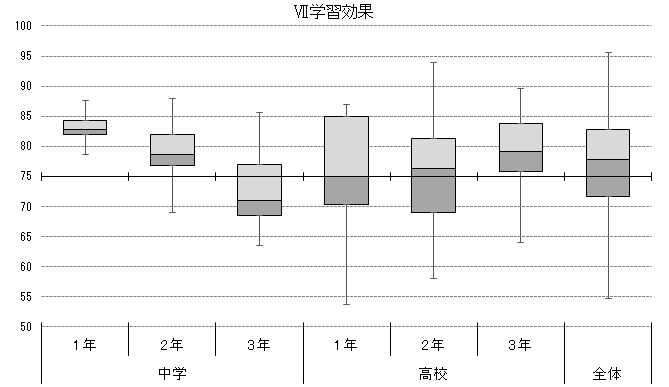
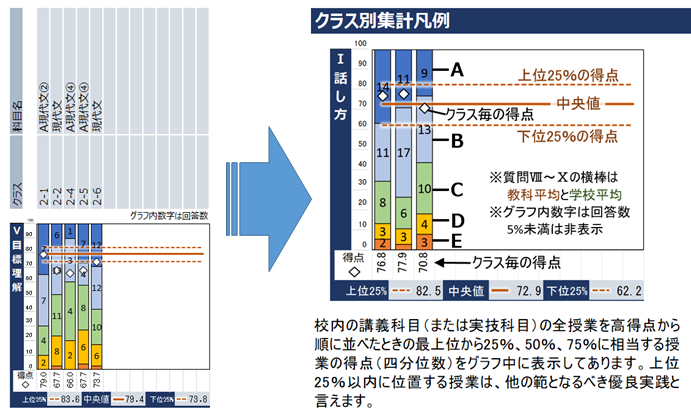
個人票(授業評価集計)の裏面には、担当する授業ごとの回答分布と換算得点の相対的な位置を表示するグラフ(下図)が掲載されています。
ご担当するクラスの得点が◇で表示されており、得点順位で上位25%、中央値、下位25%の位置を示す横線との位置関係から、担当クラスごとに相対的にどのような評価を得ているかがわかります。
もし、上位25%に相当する値(第3四分位数)を超えているなら、その授業は実践を発信すべき「優良実践」である可能性が高いはずです。教科/学校全体での授業改善を加速させるべく、当該授業での実践を積極的に発信していくことが期待されているとお考えください。
同じように教えても、同じクラスごとに集計値は異なっているのが普通です。生徒による授業評価は、担当クラスの生徒が備える学習者としての特性と先生の教え方のマッチングの度合いを示すものだからです。
高い評価を得たクラスはマッチングの度合いが高く、低かったクラスではやり方にアレンジが必要ということです。なぜ、このクラスは評価が高く、こちらのクラスは低いのかと考えてみることは、生徒を観察してより良く理解するための知見を得る好機になります。
❏ データをより精緻に見るなら「項目別学年比較」
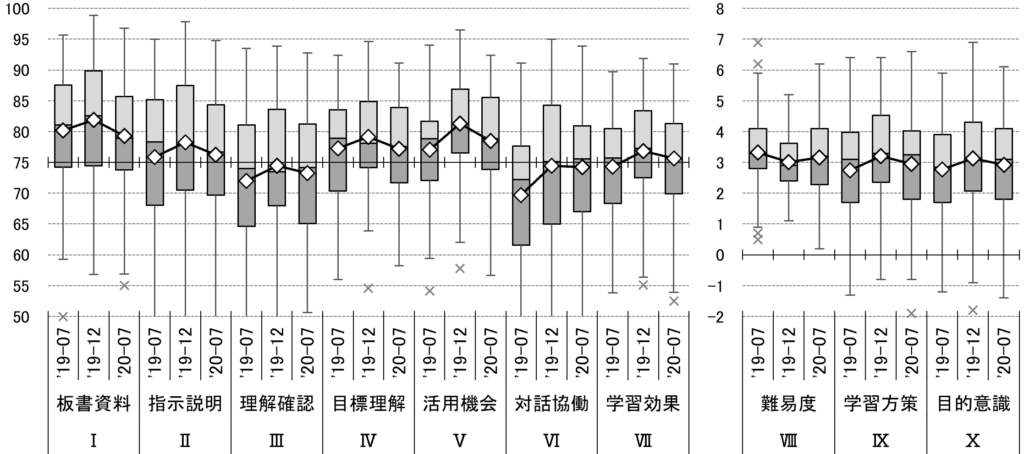
授業評価&生徒意識アンケートの納品物には、教科別団体帳票というべき「項目別学年比較」(オプション)があり、全授業の集計値の学年別分布を項目ごとに表示した「箱ひげ図」(下図)が提供されます。
箱ひげ図は、集計対象となる全授業の得点分布を度数で四等分した点を表示するグラフで「四分位グラフ」とも言います。ひげや箱の端はそれぞれ以下の数値をその位置で表しています。
| 上方に伸びたひげの先端 | 最高点(トップ) |
| 箱の上端(第3四分位数) | 得点順位でトップから25% |
| 箱内の境界線(中央値) | 得点順位でトップから50% |
| 箱の下端(第1四分位数) | 得点順位でトップから75% |
| 下方に伸びたひげの下端 | 最小値(最下位) |
なお、上記帳票では「ひげの長さは箱の長さの 1.5 倍まで」とし、その範囲に収まらない授業は「外れ値」としてひげの外に表示します。
上の例でみてもご推察いただける通り、評価結果の分布は学年ごとにも小さからぬ差があり得ます。中学入学直後は高い評価であっても、学習内容が高度化するにつれて厳しい局面を迎え、選択科目の履修がメインになる上級学年でようやく評価結果が回復するといった具合です。
しかしながら、同一学年の中でも評価の結果は異なります。上例(ある学校での実データ)でも、最も苦戦している中学3年でも80ポイントを超える授業もあれば、60ポイント台前半に止まる授業も存在します。
学年ごとに特徴的な学習内容にマッチした学ばせ方が存在したり、その学年を迎えるまでの指導で獲得させた個人/集団としての学習方策などが違いを生んでいる要因だと考えられます。
こうした評価結果の違いから、倣うべき実践として「そこで行われている手法を研究すべき授業」を特定することもまた、授業評価アンケートを行うことの大きな目的の一つです。
❏ 経年変化や目的変数への寄与度にも注目
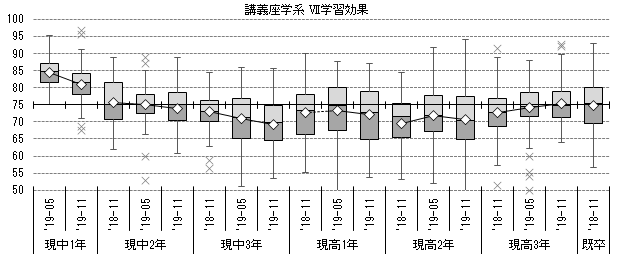
以下のグラフ群は標準的な納品物には含まれず、別途、集計結果分析をご用命いただいて提供しているものですが、集計値分布の変化を経年的に把握することで、今後に向けた改善課題が特定できたり、これまでの取り組みの成果を確かめたり、様々な活用が可能になります。
前回よりも箱の上端が高くなっていれば、先生方の創意工夫でさらに優れた手法が生み出され、教科内に定着しつつあることが示唆されます。好適実践の共有が進めば、箱の下端がせり上がり、差が縮小します。
下図を用い、同一学年の集計値分布を追えば、各時期における「指導の接続」が上手く機能しているかどうかも、ある程度まで推測できます。
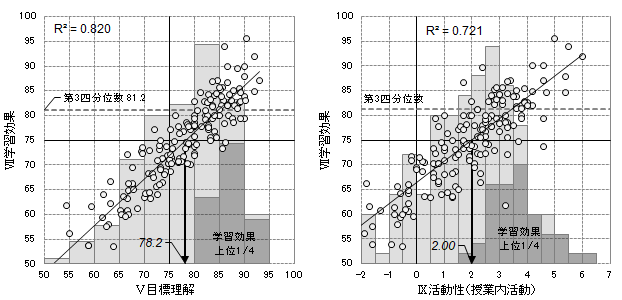
また、目的変数(学習効果)への寄与度の大きい項目に着目して作成した下図(説明変数のヒストグラムに散布図を重ねたもの)からは、その項目での改善を推し進めるべきか、他にあるボトルネックの解消を優先すべきかの判断もつきます。(cf. 散布図中の位置で探る改善課題)
このシリーズのインデックスへ
教育実践研究オフィスF 代表 鍋島史一