前稿「生徒意識調査の集計結果」でも書いた通り、「生徒に期待する行動」を明確に打ち出せているかどうかで、他項目の評価にも影響が及びます。特に「公平な指導」とは、後掲の通り、強い相関がみられます。
期待する行動とは「生活、学習、進路の各場面ででどう行動すべきか、どうなって欲しいか」を指しますが、言い換えるなら、各領域における現時点(学年・学期)及び近い未来に達成すべき状態(目標)です。
これらをしっかり共有すれば、生徒の頑張りに方向性が生まれますし、振り返りにも明確な「基準」を持てるため、行動の改善も進みます。
❏ 期待を伝える前に、指導者側での目線合わせをしっかり
伝えるべき期待となるのは、クラス担任の個人的な「思い」ではなく、学校の教育方針や学年団が共有する時期に応じた重点目標などです。
十分に議論を重ねて、学校全体/学年内で目線を合わせておかないと、方針のばらつき、基準のなさを印象付けるだけにもなりかねません。
下左図を見る限り、Q02期待する行動で十分に高い評価を得ていれば、Q03公平な指導で極端に厳しい評価を受けることはなさそうです。(但し、逆方向の因果「不公平を感じさせる場面が多いと、懐疑的な姿勢を持たれ、指導方針が伝わらなくなる」も想定されます。)
別稿「教育目標や指導方針をちゃんと伝える」でも書きましたが、指導設計に込めた思いは「あらかじめ」しっかりと伝えることが重要です。
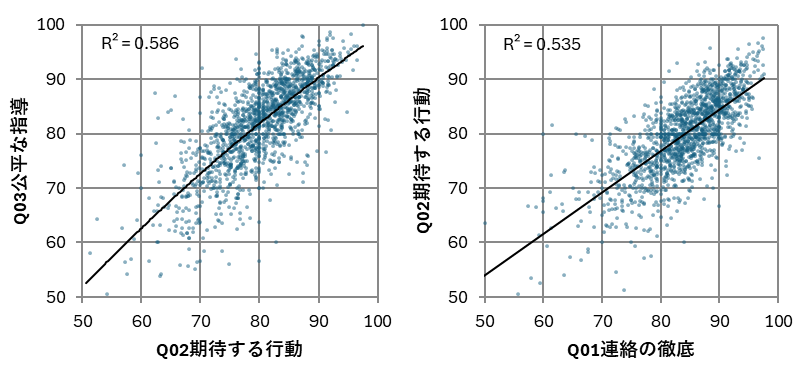
また、上右図(「連絡の徹底」との相関図)でも比較的強固な相関が見て取れます。連絡事項にせよ、期待する行動にせよ、伝えるべきことをきちんと伝える姿勢や意識は、その重要性への認識であり、事前の議論や目線合わせの不足は、その低下を招くということでしょう。
上から降りてきただけのものには、コミットの姿勢も生まれにくいはずです。方針を確立する過程できちんと意見を拾っているか、エビデンスによって必要性を伝えられているかどうかも問われるところです。
❏ 生徒の成長に合わせて、「期待」も常に更新
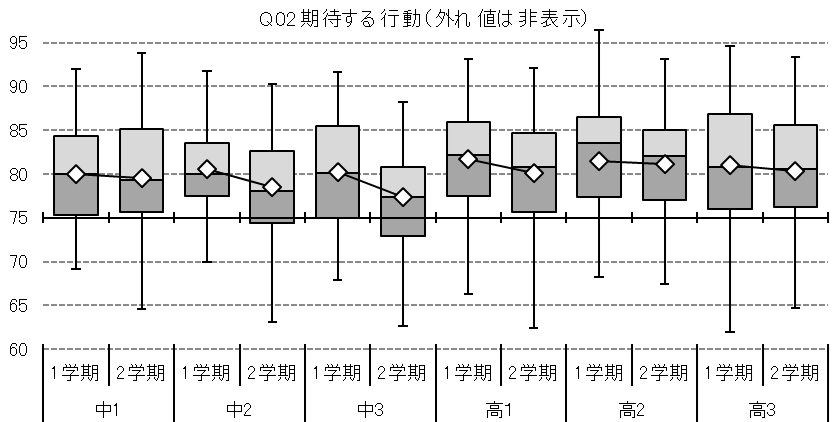
下図(Q02期待する行動の学年別の集計値分布)を見ると、どの学年も1学期よりも2学期の方が低下する傾向がみられます。
年度冒頭のオリエンテーションなどで伝えたことは、時間の経過とともに生徒の意識から揮発しがちです。繰り返して伝える必要があります。
また、指導を重ねる中で「目指すべき到達状態」が実現に近づいてきたら、「期待」をもう一歩先のものに更新する必要もあるはずです。
3年間/6年間を見渡した指導計画の中で、各時期(学年や学期)において到達を目指すものを段階的に記述した上で、生徒の成長/行動の変容がどこまで進んだら次の期待を打ち出すかも計画しておきましょう。
更新のタイミングを逸しないためには、日々の指導の中で、観察と評価を欠かさないようにするのが重要であるのは言うまでもありません。
❏ 振り返りの基準としての「期待する行動」
改めて項目間の相関(再掲)を確認すると、Q02期待する行動との間に強い相関が読み取れるのは、Q01連絡の徹底、Q03公平な指導ですが、これに加えてQ09行動選択との間にも大きめの偏相関が観測されます。
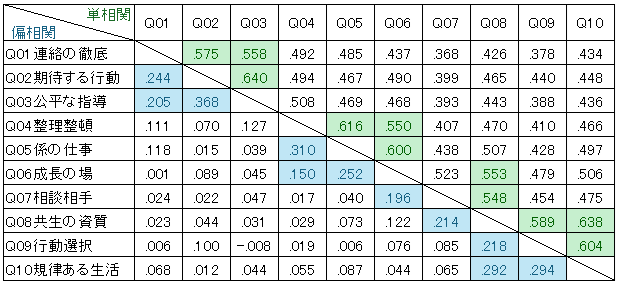
もう少し詳しくデータを解析(クロス集計)してみると、下表の結果が得られました。Q02期待する行動で、B以上を選ばないと、Q09行動選択の換算得点は75ポイント(目標値)に届きません。
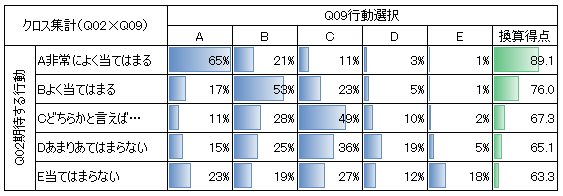
繰り返しになりますが、生活、学習、進路(加えて、探究活動や学校行事など)の各領域で、生徒に期待する行動や姿勢、態度などを言語化して伝えることは、取り組みや活動の方向を示し、活動や自分自身の言動を振り返るときの「基準」を持たせることにも繋がっていきます。
足りないところを明確に認識できれば、それを補うために何をどう頑張るべきかを考えますので、学習のみらなず、あらゆる行動を改善していくことも、より容易になっていくはずです。
相手(生徒)により良い行動をとってもらいたいなら、振り返りの機会と基準を正しく用意した上で、問い掛けながら、内省を促していくことが大切です。(cf. 相手に行動や態度の変容を促すとき)
また、反省点や改善課題だけでなく、進捗(自分の進歩)を基準に照らして捉えられれば、達成感を得て、さらなる頑張りへの欲求を膨らませるはずです。こうした好ましい循環の中に生徒を置くにも、学年や学期に応じた「期待する行動」の打ち出しは重要な部分を占めます。
❏ 期待の伝達が好ましい行動に導く効果は学年で異なる
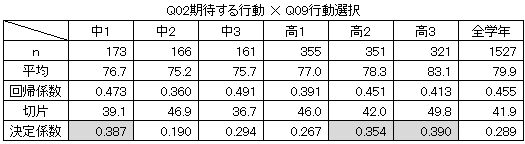
下表は、Q09行動選択を目的変数とする回帰分析の結果(要約)です。特に注意してみるべきは回帰係数と決定係数の大きさです。
回帰係数が大きければ、Q02期待する行動の充実を図ったときに、Q09行動選択の改善がより大きく見込めるということであり、決定係数の値が大きければ、その確率も高いと考えることができます。

決定係数(編み掛けを施した部分)を見ると、中1は大きな値です。先生の言葉を素直に受け止め、それに応える姿勢の表れでしょうか。
その後、中間学年では決定係数が低下し、高2や高3になって上昇します。成長を遂げた結果、先生の言わんとするところをより深く理解し、自らの行動に取り込めるだけの能力を得たということかもしれません。
高3は回帰係数(散布図で近似線を描いた場合のその傾きの大きさ)がやや小さい値ですが、その代わり切片(y=ax+b の b)は大きめ。自らの内に「行動選択の原理」を備えるようになり、先生方の指導の影響を受けずとも、自律的に自分の行動をデザインできるようになっているのだとすれば、生徒の成長を喜んで良いのではないでしょうか。
教育実践研究オフィスF 代表 鍋島史一
